Equilibrio Hardy-Weinberg
Una rama de la genética bastante teórica con grandes dosis de matemáticas y estadística es la genética de poblaciones. Se ocupa del estudio y la predicción de las variaciones y la distribución de la frecuencia de los alelos de un gen con el fin de dar una explicación a lo que conocemos como proceso evolutivo.
Uno de sus pilares es el equilibrio de Hardy-Wienberg (H-W), establecido en 1908. Supone una explicación teórica a un fenómeno natural observable, aunque se puede desarrollar matemáticamente para acercarse todavía más a la realidad.
Definición: La frecuencia o la probabilidad de que cogiendo al azar un individuo de esa población tenga un genotipo determinado, estas frecuencias son constantes entre generaciones y se mantiene en equilibrio mientras duren las condiciones. El equilibrio H-W relaciona la frecuencia génica (la frecuencia con que un alelo de un gen se encuentra en la población), con la frecuencia genotípica (la frecuencia con que una combinación de alelos se encuentra en la población).
Expresión matemática: el equilibrio H-W se basa en que:
1=p +q
1= p^2 + 2pq + q^2
Donde p es la frecuencia génica (del alelo) A y q la frecuencia génica de a.
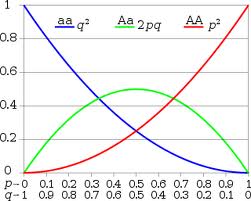
La frecuencia de cada genotipo aa (q^2), aA (2pq) y AA (p^2) (azul, verde y rojo respectivamente) están en equilibrio, para valores entre 0 y 1 de p y q ( frecuencia de los alelos)
Un ejemplo: supongamos una población de 100 guisanteras que dan guisantes amarillos y verdes de Mendel. Gracias al equilibrio H-W podemos decir cuántos saldrán amarillos o verdes en la próxima generación, si gracias a Mendel podíamos saber de qué color sería la descendencia de dos individuos, con el equilibrio de H-W podemos saberla de toda una población. No planta por planta, pero si sabemos la frecuencia de guisantes amarillos en la generación 0, podemos saber qué frecuencia de guisantes amarillos habrá en la generación 1.
La verdad es que el equilibrio H-W, no funciona exactamente en condiciones naturales, necesita que se den algunas “circunstancias” que en la naturaleza son poco probables.
Todos los individuos de la población deben ser diploides, el carácter de estudio debe estar igual repartido en ambos sexos (no puede estar en un cromosoma sexual, que no tienen una repartición igual).
La población debe ser panmictica, es decir, los individuos deben reproducirse al azar con cualquier miembro de la población (incluidos ellos mismos).
La población debe ser muy grande. Los valores individuales de los individuos en una población enorme tienen muy poco valor individual y por eso permite minimizar las diferencias para el carácter de estudio entre individuos cogidos al azar. Si coges mil personas su altura se distribuirá siguiendo una distribución normal o gaussiana (la más frecuente en fenómenos naturales), si se cogen solo cinco posiblemente no se vea una distribución porque no hay datos suficientes.
La población no debe estar sometida a procesos de mutación, migración o selección natural. Si aparecen mutaciones no se mantienen las frecuencias de los alelos que estamos estudiando. Si entran individuos nuevos pueden llevar cualquiera de los alelos para dicho gen y por lo tanto se escapan a la suposición matemática del equilibrio H-W. Una enfermedad que mata a todos los altos está sesgando la realidad de esa población (seleccionando a los bajos) y por lo tanto desbaratando la distribución de la población. Por suerte la modelización matemática permite estudiar poblaciones con una tasa de mutación conocida, o con migración o selección natural, siempre y cuando se pueda asignar un valor a esas variables.
Si una población cumple estos requisitos la frecuencia de cada alelo de un gen y la frecuencia de cada genotipo, se mantiene constante a través de las generaciones.
